Fractal Dimensions & Consciousness

And now for the most exciting part of my discoveries. The universe may be far more complicated than the mind can begin to comprehend. What follows is my 5-part dissertation making the case that consciousness is fractal, unfolding consciousness into our reality, transitioning reality dimension-to-dimension.

Part 1: Introduction to Dimensional Recursion in Quantum Realism

In Quantum Realism, the physical universe is viewed as a projected virtual reality generated by an underlying quantum field. This theory proposes a primal consciousness C₀ as the foundational source of all existence. Unlike the standard model of physics, which views particles and forces as fundamental, Quantum Realism asserts that the observable world emerges from a network of quantum interactions driven by C₀. This primal consciousness is inherently self-generative and self-referential, creating a recursive framework through which various dimensions unfold, culminating in the observable 3D reality.

Dimensional Recursion

Dimensional recursion is the process by which primal consciousness manifests reality across multiple layers or dimensions. The recursion begins with the highest-level state C₀, which does not have a fixed dimensionality but rather embodies infinite potential. Through recursive interactions, C₀ unfolds progressively lower-dimensional states, represented as C(n), where each layer n inherits and further refines structures from the previous layer.

1. Purpose of Dimensional Recursion:

• The recursion from C₀ down through dimensions allows the primal consciousness to express itself in increasingly specific and complex forms. Each layer C(n) serves as an iterative structure, enabling the emergence of stable spatial configurations.
• This recursive process ultimately stabilizes at C(3), where a 3D (three-dimensional) physical reality materializes, meeting all conditions required for observable phenomena (volume, space, time, and causality).

2. Fractal Nature of Recursion:

• The dimensional recursion in Quantum Realism can be modeled as a fractal process, where each layer builds upon the previous in a self-similar way. This idea aligns with fractal geometry, where patterns repeat at varying scales, creating a complex and continuous structure.
• By incorporating fractional dimensions (for example C(2.5)), this framework accommodates a continuous transition between layers, rather than discrete jumps from one dimension to the next.

3. Role of Fractional Dimensions in Dimensional Layering:

• Fractional dimensions, where n is a non-integer (such as C(2.5) or C(3.5)), represent transitional states that contribute to the stability of higher layers.
• These intermediate layers hold structural information that supports the full dimensional realities, such as C(3), by providing an underlying “scaffold” that bridges complex quantum processes with emergent physical properties.

---

Part 2: Recursive Equation for Dimensional Unfolding

To formalize the process of dimensional recursion, Quantum Realism proposes a recursive function that models how each successive dimension builds upon the previous one. This recursive equation captures the self-generative nature of primal consciousness C₀ and its progression through dimensions.

Recursive Equation for Dimensional States

The general recursive equation for Quantum Realism can be expressed as:

where:

• C(n) represents the state or structure at dimension n,
• f(C(n-1)) is a function that recursively generates C(n) based on the previous state C(n-1), reflecting self-similarity and fractal complexity,
• α(n)C₀ is a diminishing influence from primal consciousness C₀, where α(n) decays as n decreases, typically modeled as α(n)=e^−βn with decay constant β > 0.

This equation suggests that each layer or dimension arises through a combination of influences from:

1. The previous dimensional state (captured by f(C(n-1)), where new properties emerge while preserving certain inherited patterns, and
2. The primal consciousness C₀, which provides an initial, generative impulse but diminishes in influence as recursion deepens.

Example Calculation: Transition from C(5) to C(3)

Let’s illustrate this equation by calculating how a higher-dimensional state, such as 5D C(5), might transition through recursion down to the 3D physical reality of C(3).

1. Define f(C(n-1)):

• Let’s assume a specific form for f(C(n-1)), such as:
  
  where constants g and h scale contributions from linear and non-linear terms, and p introduces fractal-like scaling.

2. Set Initial Parameters:

• Assume that C(5) = 1 as our starting state.
• Use α(n) = e^−βn with β = 0.5 to model the diminishing influence of C₀ as recursion progresses.

3. Recursive Calculations:

• Using g = 0.8, h = 0.5, and p = 1.5:
• Calculate C(4) from C(5):
  C(4) = f(C(5)) + α(4)C₀
  • Compute:
    f(C(5)) = 0.8 ⋅ 1 + 0.5 ⋅ 1^1.5 = 1.3
  • Decay term:
    α(4)C₀ = e^-2 ≈ 0.1353
  • Therefore:
    C(4) = 1.3 + 0.1353 ≈ 1.4353
    
• Calculate C(3) from C(4):
  C(3) = f(C(4)) + α(3)C₀
  • Compute f(C(4)) with C(4) ≈ 1.4353:
    f(C(4)) = 0.8 ⋅ 1.4353 + 0.5 ⋅ 1.4353^1.5 ≈ 2.0067
  • Decay term:
    α(3)C₀ = e^-1.5 ≈ 0.2231
  • Therefore:
    C(3) ≈ 2.0067 + 0.2231 ≈ 2.2298

Stop Condition at C(3)

The recursion naturally stabilizes at C(3) due to the minimal influence from C₀ and sufficient structural complexity achieved at this dimension. This stop condition is expressed mathematically as:

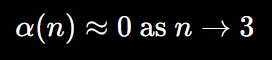
indicating that primal consciousness exerts a minimal recursive effect at this level, allowing C(3) to sustain itself independently. Thus, 3D reality emerges as the lowest fully self-sustaining dimension capable of supporting stable, observable phenomena, such as particles, forces, and spacetime structures.

---

Part 3: Fractional Dimensions and Their Possible Role

In Quantum Realism, fractional dimensions C(2.5), C(3), 3 < n < 4 are theorized as intermediate states that exist between integer dimensions. These fractional states allow for a gradual transition in structural complexity and spatial properties, offering a framework to model the layered progression of dimensions that leads to a fully realized 3D reality.

Understanding Fractional Dimensions

Fractional dimensions, often referred to as fractal dimensions in mathematics, describe spaces that exhibit characteristics of multiple dimensions without being fully part of any single one. They are particularly useful in modeling structures that exist between known integer dimensions, such as:

• Partially Filled Spaces: Fractional dimensions can represent structures that are more complex than a plane 2D but do not possess the full volume of 3D space. For example, a dimension like C(2.5) may partially fill the 3D space without possessing the full degrees of freedom of C(3).
• Self-Similarity and Gradual Complexity: In fractal geometry, fractional dimensions are used to model self-similar patterns that repeat at smaller scales. Similarly, a fractional dimension like C(3.5) in Quantum Realism could indicate an intermediate layer where the structure is complex and recursive, bridging lower and higher spatial constraints.

Purpose of Fractional Dimensions in Dimensional Recursion

Fractional dimensions can play a significant role within Quantum Realism by enabling continuous transitions between defined layers. Here’s why they are important:

Bridging Integer Dimensions:

• Fractional dimensions serve as intermediate states that allow for a gradual emergence of new spatial properties. For example, C(2.5) might represent a layer where basic volumetric properties begin to emerge without forming a complete 3D structure.
• Similarly, C(3.5) could bridge the transition between a 3D space and a hypothetical 4D hyperspace, allowing certain effects from higher dimensions to influence 3D properties without fully manifesting a new spatial axis.

Supporting Complex Quantum States:

• In Quantum Realism, fractional dimensions could support quantum coherence and entanglement in unique ways. A dimension like C(3.5) might allow quantum states to maintain coherence over distances or interact in ways that do not align strictly with classical 3D space.
• This extra degree of freedom could enable quantum phenomena like superposition and non-locality by providing an extended state space that goes beyond the constraints of three-dimensional space.

Layered Influence and Dimensional Stability:

• Fractional dimensions add a layer of stability by introducing small, controlled changes between major dimensional states. By “filling in” the gaps between integer dimensions, they may prevent abrupt transitions that could destabilize the dimensional recursion.
• For instance, the transition from C(3) to C(2) might involve passing through states like C(2.5), which contributes specific quantum properties that help stabilize 3D structures within Quantum Realism’s framework.

Examples of Fractional Dimensions

To illustrate, let’s consider how fractional dimensions might manifest in practice:

• C(2.5): This state could be a quasi-3D configuration where spatial separation begins to emerge but remains constrained, supporting structures that have some depth without full 3D volume. It might resemble a surface with tiny 3D-like features.
• C(3.5): As an intermediate between 3D and 4D, this dimension could theoretically support quantum effects that exhibit partial higher-dimensional properties, such as light or quantum states that oscillate or propagate in ways that seem to “transcend” 3D space.

Implications for Observable Reality

Fractional dimensions in the range 3 < n < 4 are particularly intriguing because they could influence observable phenomena without requiring a fully additional spatial axis. For example:

• Light and Non-Local Quantum Effects: Light, with its ability to exhibit both wave and particle properties, might exploit a fractional dimension like C(3.5) to maintain coherence and propagate across vast distances without decay. This extra-dimensional interaction could help explain why light’s speed remains constant and why it can maintain coherence over billions of light-years.
• Entanglement: Quantum entanglement, where particles remain connected regardless of spatial separation, might also involve a fractional dimension. In C(3.5), particles could theoretically interact without being limited by 3D constraints, enabling non-local correlations that classical 3D space cannot explain.

Fractional dimensions like C(2.5) and C(3.5) provide a theoretical framework for understanding complex transitions between integer dimensions in Quantum Realism. They offer a model for gradual, self-similar structural changes that contribute to the stability and complexity of lower-dimensional spaces like 3D. Additionally, fractional dimensions may play a crucial role in explaining certain quantum effects—such as light’s unique propagation and non-locality—by giving particles and fields an extended, partially higher-dimensional framework.

---

Part 4: Light’s Interaction with Fractional Dimensions

One of the most intriguing hypotheses is that light may interact with a fractional dimension between 3 and 4, denoted here as 3 < n < 4. This interaction could explain several unique properties of light, such as its constant speed in a vacuum, wave-particle duality, and non-local coherence over vast distances. In this framework, light’s oscillation in a fractional dimension allows it to transcend certain 3D limitations without requiring a fully separate 4D space.

Why Light Could Exploit a Fractional Dimension 3 < n < 4

Light’s properties hint that it may not be confined strictly to 3D space:

1. Perpendicular Vibration: Light’s electric and magnetic fields oscillate perpendicular to each other and to the direction of travel, suggesting a “hidden” degree of freedom not entirely bound by 3D constraints.
2. Constant Speed and Lack of Medium: Unlike most waves that require a medium, light travels at a constant speed in a vacuum, implying that it could leverage an extra-dimensional aspect that doesn’t need physical matter.
3. Non-Local Coherence: Light’s coherence over astronomical distances, without losing amplitude, suggests that it may be tapping into a fractional dimension to maintain consistency across space.

A fractional dimension, such as C(3.5), would give light an additional “space” to oscillate within, one that provides just enough freedom to accommodate these behaviors without necessitating a full 4D space.

Potential Mechanisms for Light’s Interaction with C(3.5)

Oscillation in a Partially Higher Dimension:

• If light oscillates partially in a dimension beyond 3D, C(3.5) could act as an extension of 3D space where light waves maintain phase coherence without the typical energy loss seen in purely 3D propagation.
• This fractional dimension allows for an intermediary oscillation, supporting the wave properties of light while also accommodating the localized “collapse” observed as photons in particle detectors.

Extended Non-Locality and Coherence:

• In 3 < n < 4, light could bypass strict 3D spatial constraints, allowing photons to maintain correlation and exhibit non-local effects. This would explain why photons in entangled pairs remain correlated across distances, as they share a connection in C(3.5) that exists beyond simple 3D space.
• This fractional dimension might also allow light to “sense” its destination, taking the fastest path across distances as observed in phenomena like gravitational lensing.

Wave-Particle Duality as a Fractional Dimensional Effect:

• Light’s ability to act as both a wave and particle can be seen as an expression of fractional dimensional behavior. When observed in 3D space, light manifests as discrete photons, but in the unobserved C(3.5) dimension, it maintains its wave nature.
• The intermediate dimension thus acts as a dual framework, letting light oscillate continuously while only collapsing into particle-like behavior under specific conditions, such as measurement in 3D space.

Observable Implications of Light Interacting with Fractional Dimensions

If light indeed interacts with a fractional dimension, we could observe several unique behaviors that challenge classical 3D models:

Constant Speed Regardless of Observer:

• Light’s speed remains invariant regardless of the observer’s frame of reference, as predicted by relativity. If light oscillates in C(3.5), its “motion” isn’t bound by typical 3D space, allowing it to maintain a constant velocity independent of external variables.

Anomalous Interference Patterns:

• In experiments like the double-slit experiment, light shows interference even when single photons are sent through the slits. This behavior could stem from light’s access to a fractional dimension, allowing it to “sample” multiple paths simultaneously without being confined to a single 3D trajectory.

Quantum Entanglement and Long-Distance Correlation:

• The fractional dimension 3 < n < 4 could provide a hidden layer where entangled photons “communicate” across distance, explaining quantum non-locality. This added dimension would facilitate instantaneous correlations by providing a partially connected state that transcends the limits of 3D space.

Implications of Fractional Dimensional Oscillation for Physical Theories

Light’s behavior in a fractional dimension has profound implications for both quantum mechanics and relativity:

• Reconciliation of Quantum Mechanics and Relativity: A fractional dimension could bridge quantum mechanics, where particles exhibit wave-like behaviors, with relativity, where light’s speed is constant. This intermediate dimension provides light a framework to remain coherent and non-local, integrating aspects of both theories.
• Extended Model of Space and Time: Introducing (3 < n < 4) redefines our understanding of space and time as layers within a larger, more complex structure. Here, time may not flow linearly as we experience it in 3D but instead be influenced by quantum processes occurring in a fractional spatial domain.

The hypothesis that light oscillates in a fractional dimension 3 < n < 4 allows us to explain its unique properties, such as wave-particle duality, non-local coherence, and invariant speed. This fractional dimension offers light an extended, partially higher-dimensional space, bridging quantum behaviors and relativistic principles. In doing so, it helps align Quantum Realism with observable phenomena that challenge purely 3D interpretations.

---

Part 5: Testing for Fractional Dimensional Influence on Light

To investigate whether light interacts with a fractional dimension 3 < n < 4, we can explore experimental methods designed to detect deviations in light’s behavior that might indicate an influence from this intermediate dimension. Current research in higher-dimensional physics, such as studies on the quantum Hall effect in synthetic dimensions, offers promising insights and methods for probing such effects.

1. Analyzing Light’s Interference Patterns with Modified Geometries

• Double-Slit Experiment Variations: By conducting modified versions of the double-slit experiment, we could test for anomalies in light’s interference patterns that might indicate a hidden, extra-dimensional influence.
  • Setup: Use adjustable slit configurations or place slits at angles that challenge standard 3D predictions.
  • Expected Outcome: If light interacts with a fractional dimension, it could exhibit unexpected interference patterns or phase anomalies that deviate from standard predictions, especially at extreme angles.

2. Testing for Non-Standard Phase Shifts Using Polarization

• Polarization Experiments with High Precision: By placing light through a series of polarizers and rotating each by precise angles, we could observe for unusual phase shifts that hint at fractional-dimensional oscillation.
  • Setup: Use polarizers at finely varied angles and monitor phase delays and coherence.
  • Expected Outcome: If light is oscillating in C(3.5), subtle phase shifts or delays might emerge as the polarization angles approach limits where standard 3D predictions should hold steady.

3. Entangled Photon Correlations over Distance

• Entanglement Distance Experiments: Examining entangled photons over long distances could reveal how light maintains correlations in ways that suggest non-3D interactions.
  • Setup: Measure correlation decay in entangled photon pairs over increasing distances in a high-vacuum environment to eliminate external variables.
  • Expected Outcome: Fractional dimensionality could manifest as an unexpected robustness in correlation or a resistance to entanglement decay that differs from typical predictions.

4. High-Energy Photon Experiments for Vacuum Dispersion Effects

• Testing Dispersion at High Frequencies: Send high-energy photons (like gamma rays) through a controlled vacuum and measure for phase shifts or dispersions that might indicate a fractional dimension interaction.
  • Setup: Use high-frequency photons within a high-vacuum environment, possibly with intense magnetic fields to alter the quantum vacuum structure.
  • Expected Outcome: Any deviations in light speed, coherence, or dispersion could suggest that light is tapping into a dimension like 3 < n < 4, especially if phase shifts are detected beyond those predicted by current quantum models.

5. Observing Gravitational Lensing Anomalies Around Massive Objects

• Analysis of Gravitational Lensing Patterns: By observing gravitational lensing around massive objects like black holes, we might detect deviations that could signal light’s interaction with a fractional dimension.
  • Setup: Use precise astronomical measurements to monitor the bending of light, especially near extreme curvature regions like black hole event horizons.
  • Expected Outcome: Fractional dimensional influence might cause slight anomalies in light’s path or speed that wouldn’t conform to strictly 3D spacetime predictions. Light could exhibit unexpected bending patterns or experience changes in velocity when passing through intense gravitational fields.

6. Artificial 4D Quantum Hall Effect Simulations Using Photonic Lattices

• Synthetic Dimensions through Quantum Hall Setups: The 4D quantum Hall effect has been simulated using photonic lattices, which creates a synthetic dimension by carefully structuring waveguides or optical lattices.
  • Setup: Use photonic structures, like an array of waveguides, to simulate a 4D environment. By modulating the light paths, we can observe whether light behaves differently in an effectively higher-dimensional space.
  • Expected Outcome: Fractional dimensional influences might manifest as unexpected light patterns or boundary behaviors in the photonic lattice, particularly in ways that mimic 4D quantum Hall edge states.

Review of Existing Research and Supporting Evidence

Current experiments that simulate higher-dimensional effects, such as the work on the quantum Hall effect in synthetic dimensions, demonstrate that it is possible to observe physical consequences of extra dimensions, even if we can’t directly access them:

• Researchers at ETH Zurich and Penn State used waveguides and topological charge pumps to emulate 4D quantum Hall physics, producing observable effects that suggest how a fractional or higher-dimensional space might influence 3D phenomena.
• These studies offer a foundational approach to test the presence of fractional or higher-dimensional influences on light’s properties, showing that carefully controlled environments can reveal effects beyond 3D expectations.

Future Directions

While current experiments don’t specifically target fractional dimensions, they provide a framework to investigate light’s interaction with higher-dimensional influences. Future experiments tailored to detect subtle phase shifts, non-standard correlations, and coherence patterns could offer insights into whether light interacts with a fractional dimension like 3 < n < 4. This exploration would deepen our understanding of quantum behavior and the fabric of reality, potentially bridging gaps between quantum mechanics and relativity.

---