Quantum Realism, Consciousness, Fractals, and the Golden Ratio: A Unified Model
by Joseph Gonzalez, Oct 2024 (BantamJoe)
This is the culmination of my life’s work. Understanding and formulating a theory of reality and consciousness. All the math is my math. I’ve borrowed from many philosophers, scientists and engineers, to formulate my own interpretation of the universe. Everything written and developed is foundationally in harmony with quantum mechanics, the physical laws of reality, information science, and is mathematically and logically sound. I hope you enjoy this.
Quantum Realism (QR) proposes that the universe operates as a reality generated by a quantum field network. Consciousness, in this framework, emerges from the recursive processing of quantum states within this network. This dissertation explores how fractal geometry, the Fibonacci sequence, and the golden ratio ϕ play a role in the recursive and self-similar processes that underpin both quantum reality and the emergence of consciousness. Through a detailed examination of recursive quantum states and their mathematical properties, we demonstrate how these mathematical patterns can model the growth and complexity of consciousness.
1. Introduction to Quantum Realism and Consciousness
Quantum Realism (QR) posits that the physical universe is a reality generated by a vast network of quantum nodes processing information at the quantum level. This view shifts our understanding of the universe from one of material objects governed by classical mechanics to one driven by the processing of quantum information. In QR, matter, space, and time are all emergent properties of this underlying quantum field network. Similarly, consciousness is viewed not as a byproduct of brain activity but as an intrinsic aspect of quantum processing.
The goal of this dissertation is to model how consciousness might emerge from the recursive interactions of quantum states within this network, utilizing fractal geometry, the Fibonacci sequence, and the golden ratio as key mathematical tools. We will explore how these concepts offer a robust framework for describing the self-similar, recursive nature of quantum processing and consciousness, drawing parallels between the growth of fractals in nature and the recursive accumulation of conscious states over time.
2. Recursive Processes in Quantum Networks
2.1. Fractals and Quantum Networks
Fractals are recursive geometric structures that exhibit self-similarity at different scales. Each smaller part of a fractal is a reduced version of the whole, and this recursive process can continue indefinitely, creating structures of infinite complexity from simple iterative rules. In a similar fashion, quantum networks process information recursively, with each quantum node interacting with others to generate increasingly complex patterns of reality.
Mathematically, fractals can be described using iterative equations, such as the Mandelbrot set:
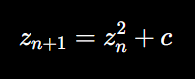
Here, z represents a complex number, and c is a constant. Iterating this equation produces the famous fractal structure known as the Mandelbrot set. In the context of QR, we propose that consciousness could arise from a similar recursive process, where each new conscious state Cn builds on the previous one, influenced by quantum states Ψn processed by the network.
2.2. Quantum Superposition and Recursive States
In QR, quantum states are typically represented as superpositions of multiple possible states:
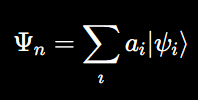
where ∣ψi⟩ represents an individual quantum state, and ai are probability amplitudes. The recursive interactions between these quantum states give rise to emergent properties, including consciousness. These interactions can be thought of as fractal-like, where each quantum state influences the next in a self-similar manner.
3. The Fractal-Based Consciousness Equation
To model consciousness in QR, we propose a fractal-based consciousness equation that captures the recursive, self-similar nature of quantum processing. The equation is structured as follows:
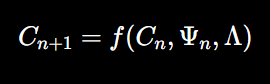
Where:
- Cn+1 represents the state of consciousness at the next iteration.
- Cn is the current state of consciousness.
- ψn is the quantum state at the current iteration, expressed as a superposition of quantum possibilities.
- Λ is the processing bandwidth or capacity of the quantum field network.
- f is a recursive function governing how the next conscious state emerges from the current one.
This equation models the recursive nature of consciousness, where each moment of awareness builds upon the previous one, incorporating new information from quantum states and constrained by the network’s processing bandwidth. The integral over Λ captures the accumulation of quantum information over time:
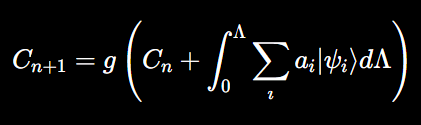
Here, g is a function that ensures only coherent quantum states contribute to the next iteration of consciousness. The recursive process described by this equation mirrors how fractals accumulate complexity by repeating simple rules across scales.
4. Role of the Golden Ratio and Fibonacci Sequence in Consciousness
4.1. The Golden Ratio as an Optimal Scaling Factor
The golden ratio ϕ, approximately 1.618, is a mathematical constant that frequently appears in systems characterized by recursive growth. It is defined as:
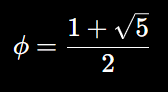
The golden ratio is often associated with optimal growth and self-organization, as it provides a balance between expansion and stability. In nature, the golden ratio appears in the arrangement of leaves, the spirals of shells, the length of segments of fingers on a hand, and the branching of trees. These are all systems that exhibit fractal-like growth, suggesting that ϕ might similarly influence the growth of consciousness.
In our fractal-based equation, we can incorporate the golden ratio as a scaling factor for the recursive growth of consciousness:
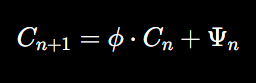
This equation suggests that each new state of consciousness grows in proportion to the golden ratio, ensuring that the recursive growth of consciousness is balanced and efficient. The golden ratio provides a natural mechanism for scaling quantum information in a way that mirrors optimal growth in biological systems.
4.2. Fibonacci Sequence in Recursive Quantum States
The Fibonacci sequence is closely related to the golden ratio. It is a recursive sequence where each term is the sum of the two preceding terms:
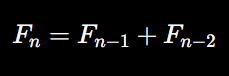
As the sequence grows, the ratio between consecutive Fibonacci numbers approaches ϕ. In QR, we propose that the evolution of quantum states could follow a Fibonacci-like recursion, where each quantum state at time n depends on the previous two states:
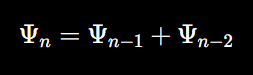
This recursive process can be integrated into the fractal-based consciousness equation to model how quantum states accumulate over time:
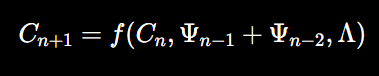
This equation reflects the Fibonacci pattern of growth, where the quantum network processes information recursively, and consciousness emerges from the sum of previous quantum states.
4.3. Mathematical Example: Recursive Consciousness with Golden Ratio and Fibonacci
We now combine these concepts to construct a detailed mathematical model for consciousness, where both the golden ratio and Fibonacci sequence play a role in the recursive growth of quantum states and consciousness:
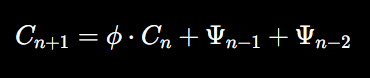
This equation captures how consciousness evolves recursively, growing according to the golden ratio and integrating quantum information in a Fibonacci-like manner. The recursive structure ensures that consciousness builds on its past states while scaling optimally, leading to increasingly complex conscious experiences over time.
5. Derivation and Implications of the Fractal-Based Consciousness Model
5.1. Recursive Derivation of Quantum States
To derive the recursive growth of consciousness, we first express the quantum state Ψn in terms of the previous states:
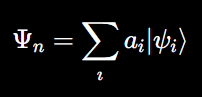
At each iteration, the superposition of quantum states evolves recursively:
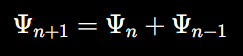
Substituting this into the fractal-based consciousness equation, we get:
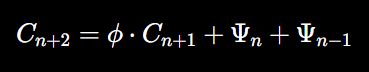
This equation recursively builds upon the previous states of consciousness, with the golden ratio ensuring optimal scaling and the Fibonacci recursion guiding the accumulation of quantum information.
5.2. Fractals, Self-Similarity, and Consciousness
The self-similar nature of fractals means that the recursive rules governing the growth of consciousness repeat at different scales. In this model, consciousness exhibits fractal-like behavior, where each new iteration reflects the structure of previous iterations, but with increasing complexity. The golden ratio ensures that this growth remains balanced, while the Fibonacci sequence provides a natural pattern for recursive accumulation.
6. Conclusion: A Unified Model for Consciousness, Fractals, and Quantum Realism
In this dissertation, we have explored how fractals, the golden ratio, and the Fibonacci sequence can provide a unified framework for modeling consciousness in the context of Quantum Realism. By incorporating these mathematical patterns into a fractal-based consciousness equation, we have demonstrated how consciousness can emerge from the recursive interactions of quantum states, growing in complexity while maintaining a balance between past and present states.
The proposed equation:
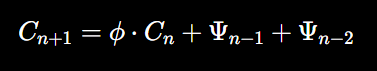
captures the recursive, fractal-like nature of consciousness, where each moment of awareness builds upon the previous one through optimal scaling and Fibonacci-like recursion. This model provides a mathematically grounded framework for understanding how consciousness arises from the underlying quantum field, offering new insights into the relationship between quantum processing, fractal geometry, and the emergent phenomenon of consciousness.












Leave a comment